Solution to previous problem and technique of geometric construction to solve inequalities

Posted on by

To solve the problem in yesterday’s post, we need to do some length chasing…

Recall that we want to find the length of BE in the diagram above. We have to find ways to express BE using the quantities that we know, which are AB, BC, AC, CD.

Let us see if similar triangles can help us simplify the problem. There are several similar triangles that we can find easily due to properties of circle, namely \triangle ABE \sim AFC and \triangle CFD \sim \triangle ABD. From the former set of similar triangles, we have:

BE = \dfrac{AB \cdot CF}{AF}

The next 2 quantities that we have to chase are CF and AF. CF can be related using the similar triangles \triangle CFD \sim \triangle ABD.

CF=\dfrac{AB\cdot CD}{AD}

which is not bad, since all these quantities are given or can be derived using Stewart’s theorem. Before plugging in the values, we try to derive an expression for AF first using power of a point theorem. We have:

AF = AD+DF= AD + \dfrac{BD \cdot CD}{AD} = \dfrac{AD^2+BD \cdot CD}{AD}

So BE = \dfrac{AB \cdot CF}{AF} = \dfrac{AB^2 \cdot CD}{AD^2+BD\cdot CD}

Right now, we can use Stewart’s theorem to derive the length of AD. You can also manipulate Stewart’s Theorem to give you the following expression:

AD^2+BD \cdot CD = \dfrac{AC^2 \cdot BD + AB^2 \cdot CD}{BC}

Hence, BE = \dfrac{AB^2 \cdot CD \cdot BC}{AC^2 \cdot BD + AB^2 \cdot CD} = \dfrac{2535}{463}

Many weeks ago I gave this problem in the first post of the blog:

Suppose x, y, z are real numbers that satisfy 0<x<y<z<\pi/2. Prove that

\dfrac{\pi}{2}+2\sin{x}\cos{y}+2\sin{y}\cos{z} > \sin{2x}+\sin{2y}+\sin{2z}

Weird problems call for weird methods. This inequality is unconventional because it contains both trigonometric function and the constant \pi/2 in the same expression. We also notice that the inequality is strict and hence it is futile to find the equality case. Let us transform the inequality into this form using double angle formula and see if it means anything:

\dfrac{\pi}{4}+\sin{x}\cos{y}+\sin{y}\cos{z} > \sin{x}\cos{x}+\sin{y}\cos{y}+\sin{z}\cos{z}

Many people may try using product to sum formulas or calculus to prove the above inequality. However, these methods will not lead to any results and are very nasty to manipulate. The key to this problem is to figure out the significance of \pi/4.

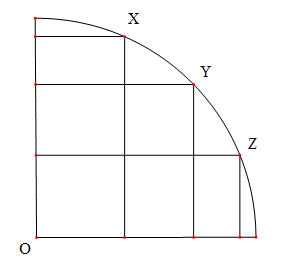
Note that \pi/4 is the area of a quarter of a circle. It seems like every term in the inequality represents some sort of area within a quarter circle. Consider the diagram below:

With this diagram, the inequality becomes more apparent. Rearranging the inequality, it gives us:

\dfrac{\pi}{4} > \sin{x}\cos{x}+\sin{y}\cos{y}+\sin{z}\cos{z}-\sin{x}\cos{y}-sin{y}cos{z}

The left hand side of the inequality is the area of the quarter circle with radius 1. The expression on the right represents the union of the areas formed by the three rectangles defined by points X,Y,Z. No matter where these three points are, the area of these rectangles will always be smaller than the area of the quarter circle!

Questions that involve geometric construction are very rare, but their proofs are very elegant and rewarding. Try proving the following inequalities with geometric construction:

1) Prove that |\sqrt{x^2+x+1}-\sqrt{x^2-x+1}<1| where x is a real number.

2) Given 100 positive real numbers x_1, x_2, \cdots, x_n that satisfy

  • x_1^2+x_2^2+\cdots+x_n^2>10000
  • x_1+x_2+\cdots x_n\le 300

Prove that there exist three numbers from this set such that the sum of these three numbers is larger than 100.

Cheers,

ksj

Leave a comment